Convex Analysis Review Notes

Or, everything you ever needed to know from… Convex analysis?

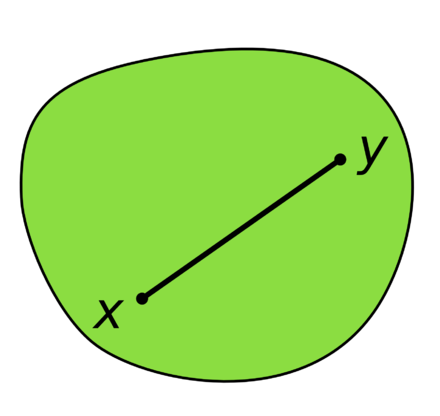
Convex Sets

Let \(S \subseteq \mathbb{R}^n\). The set \(S\) is called Convex if for any \(x_1, x_2 \in S\) and \(\lambda \in (0,1)\), it holds that

A set is convex if, from everywhere in S, all other points are visible. If two points in \(S\) are chosen, and a line drawn between them, all points on that line should also be in \(S\).

If a point \(x^* \notin S\) can be found such that \(x^* = \lambda x_1 + (1 - \lambda) x_2\), then \(S\) is not convex.

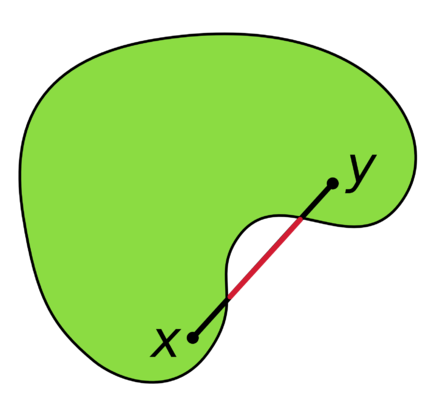
Properties of Convex Sets

• The set \(\mathbb{R}^n\) is a convex set
• The empty set is a convex set
• The set \(\{ x \in \mathbb{R}^n : \|a\| \geq a \}\) is convex for every value of \(a \in \mathbb{R}\)
• The set \(\{ x \in \mathbb{R}^n : \|a\| = a \}\) is non-convex for \(a > 0\)
• Finite sets are non-convex (why?)
• The intersection of two convex sets is also a convex set.
  
  
  

Convex and Affine Hulls and Combinations

Let \(V \subseteq \mathbb{R}^n\).

• An Affine Combination of the points \(\{ v_1, v_2, \dots v_k \}\) is a vector \(v\) satisfying:

If the weights additionally satisfy \(\lambda_i \geq 0\) for all \(i = 1 \dots k\), then \(v\) is called a Convex Combination

• The Affine Hull, denoted by \(\text{aff } V\), is the smallest affine subspace of \(\mathbb{R}^n\) that includes \(V\)
  • \(\text{aff } V\) is the set of all convex combinations of points in \(V\)
• The Convex Hull, denoted by \(\text{conv } V\), is the smallest convex set that includes \(V\)
  • \(\text{conv } V\) is the set of all convex combinations of points in \(V\)
• Carathéodory’s Theorem: Let \(x \in \text{conv }V\), where \(V \subseteq \mathbb{R}^n\). Then \(x\) can be expressed as a convex combination of \(n+1\) or fewer elements.
• Simmilarly, let \(x \in \text{aff }V\), where \(V \subseteq \mathbb{R}^n\). Then \(x\) can be expressed as a affine combination of \(n+1\) or fewer elements.

Properties thereof

• The affine hull of three or more points in \(\mathbb{R}^2\) not all lying in the same line is \(\mathbb{R}^2\) itself
• The affine hull of three or more points in \(\mathbb{R}^3\) not all lying in the same line is the plane in \(\mathbb{R}^3\) intersecting those points.
• The affine hull of an affine space is the space itself.
• The convex hull of a convex space is the space itself.

Polytopes and Polyhedron

• A subset \(P\) of \(\mathbb{R}^n\) is a Polytope if it is the convex hull of finitely many points in \(\mathbb{R}^n\)

In layman’s terms, a Polytope is the geometric structure in \(\mathbb{R}^n\) created by the convex hull \(P\). That’s still kinda confusing, so consider these examples:

• Any polygon in \(\mathbb{R}^2\) is a polytope
• A cube, a tetrahedron, and pyramids are all polytopes in \(\mathbb{R}^3\)
• circles are not polytopes in \(\mathbb{R}^2\)
• Simmilarly spheres are not polytopes in \(\mathbb{R}^3\)

A point \(v\) of a convex set \(P\) is called an Extreme Point if \(v = \lambda x_1 + (1 - \lambda ) x_2\) for \(x_1, x_2 \in P\), \(\lambda \in (0,1)\), it follows that \(v = x_1 = x_2\) In other words, an extreme point is a point that is not an interior point of any line segment lying entirely in the polytope P

This section really needs pictures, unfortunately.

• Let \(V \subset \mathbb{R}^n\) and let \(P\) be the polytope \(\text{conv }V\). Then \(P\) is equal to the convex hull of the extreme points of \(V\)

• A subset \(P\) of \(\mathbb{R}^n\) is called a Polyhedron if there exists a matrix \(A \in \mathbb{R}^{m \times n}\) and a vector \(b \in \mathbb{R}^m\) such that \(P = \{ x \in \mathbb{R}^n: A x \leq b\}\)

• Algebraic Characterization of Extreme Points: Let \(\hat{x} \in P = \{ x \in \mathbb{R}^n: A x \leq b\}\), where \(A \in \mathbb{R}^{m \times n}\) has \(\text{rank }A = n\) and \(b \in \mathbb{R}^m\). Furthermore let \(\hat{A} \hat{x} = \hat{b}\) be the equality subsystem of \(A \hat{x} = b\). Then \(\hat{x}\) is an extreme point of \(P\) if and only if \(\text{rank }\hat{A} = n\)

• Let \(P\) be a polyhedron. The number of points in \(P\) is uncountably infinite (why?). The number of extreme points of a polyhedron is finite (why?)

  • Let \(A \in \mathbb{R}^{m \times n}\) and \(b \in \mathbb{R}^m\). The number of extreme points of \(P := \{ x \in \mathbb{R}^n : Ax \leq b\}\) is less than \({m \choose n} = \frac{m!}{n!(m-n)!}\). More specifically, the number of extreme points of \(P\) never exceeds the number of \(n\) objects can be chosen from a set of \(m\) options.

• The convex hull of the extreme points of a polyhedron is a polytope.

Cones, Representation Theorem, Seperation Theorem, and Farkas’ Lemma

Cones have a special definition in convex analysis. A subset \(C\) of \(\mathbb{R}^n\) is a Polyhedral Cone if and only if \(\lambda x \in C\) for all \(x \in C\) and \(\lambda > 0\)

With this definition, we can make a few important definitions:

• Representation Theorem: Let \(A \in \mathbb{R}^{m \times n}\) and \(b \in \mathbb{R}^m\). Let \(Q := \{ x \in \mathbb{R}^n : Ax \leq b\}\), \(P\) denote the convex hull of the extreme points of \(Q\), and \(C := \{ x \in \mathbb{R}^n : Ax \leq 0^m \}\). If \(\text{rank} A = n\) then

In other words, every polyhedron with at least one extreme point (\(Q\)) is the sum of a polytope (\(P\)) and a polyhedral cone (\(C\)).

• A set \(P\) is a polytope if and only if it is a bounded polyhedron.

• Seperation Let \(C_1\) and \(C_2\) be nonempty sets in \(\mathbb{R}^n\), and let \(H := \{ x \in \mathbb{R}^n : \pi^T x = \alpha \}\) be a hyperplane in \(\mathbb{R}^n\). Then the following are true:
  • H is said to Seperate \(C_1\) and \(C_2\) if \(\pi^T x \geq \alpha\) for all \(x \in C_1\) and \(\pi^T x \leq \alpha\) for all \(x \in C_2\)
  • H is said to Properly Seperate \(C_1\) and \(C_2\) if in addition \(C_1 \cup C_2 \not\subset H\)
  • H is said to Stricly Seperate \(C_1\) and \(C_2\) if \(\pi^T x > \alpha\) for all \(x \in C_1\) and \(\pi^T x < \alpha\) for all \(x \in C_2\)
  • H is said to Strongly Seperate \(C_1\) and \(C_2\) if, for some \(\epsilon > 0 \pi^T x > \alpha + \epsilon\) for all \(x \in C_1\) and \(\pi^T x < \alpha\) for all \(x \in C_2\)
• Seperation Theorem: Suppose the set \(C \subseteq \mathbb{R}$^n\) is nonempty, closed and convex. Suppose a point \(y\) does not lie in \(C\). Then there exists a vector \(\pi \neq o^n\) and \(\alpha in \mathbb{R}\) such that \(\pi^T y > \alpha\) and \(\pi^T x \leq \alpha\) for all \(x \in C\)

In other words, if a point \(y\) does not lie in a closed and convex set \(C\), then there exists a hyperplane \(H\) that completely seperates \(y\) from \(C\)

• Let \(C \subset \mathbb{R}^n\) be a closed and convex set. Then \(C\) is the intersection all half-spaces containing \(C\)

• Farkas’ Lemma: Let \(A \in \mathbb{R}^{m \times n}\) and \(b \in \mathbb{R}^m\). Then Exactly one of the following systems has a solution, and the other is inconsistent:

  • \[Ax = b, \\ x \geq 0^n\]
  • \[A^T \pi \leq 0^n, \\ b^T \pi > 0\]

Convex Functions

Suppose that a set \(S \subseteq \mathbb{R}^n\). A continuous function \(f : \mathbb{R}^n \rightarrow \mathbb{R}\) is convex at \(\bar{x} \in S\) if for \(\lambda \in (0,1)\) and \(x \in S\),

In other words, a convex function is a function that is always “lower” than it’s linear interpolation.

From the definition, it also follows that \(f\) is convex on \(S\) if and only if, for \(x_1, x_2 \in S, \lambda \in (0,1)\),

• A function of many variables is convex or concave if it is twice differentiable.

Sources

@book{andréasson2005introduction,
  title={An Introduction to Continuous Optimization},
  author={Andr{\'e}asson, N. and Evgrafov, A. and Patriksson, M.},
  isbn={9789144044552},
  url={https://books.google.com/books?id=dxdCHAAACAAJ},
  year={2005},
  publisher={Professional Publishing Svc.}
}
@misc{ wiki:xxx,
  author = "Wikipedia",
  title = "Convex set --- Wikipedia{,} The Free Encyclopedia",
  year = "2015",
  url = "https://en.wikipedia.org/w/index.php?title=Convex_set&oldid=686390268",
  note = "[Online; accessed 25-January-2016]"
}
@misc{ wiki:xxx,
   author = "Wikipedia",
   title = "Carathéodory's theorem (convex hull) --- Wikipedia{,} The Free Encyclopedia",
   year = "2016",
   url = "https://en.wikipedia.org/w/index.php?title=Carath%C3%A9odory%27s_theorem_(convex_hull)&oldid=698633316",
   note = "[Online; accessed 25-January-2016]"
 }
 http://math.caltech.edu/Simon_Chp8.pdf
 @misc{292941,
     TITLE = {How to determine whether a function of many variables is convex or non-convex?},
     AUTHOR = {Peder (http://math.stackexchange.com/users/59704/peder)},
     HOWPUBLISHED = {Mathematics Stack Exchange},
     NOTE = {URL:http://math.stackexchange.com/q/292941 (version: 2013-02-02)},
     EPRINT = {http://math.stackexchange.com/q/292941},
     URL = {http://math.stackexchange.com/q/292941}
 }