Optimization - Linear Algebra Review

Linear Algebra Review Notes

Or, everything you ever needed to know from linear algebra.

Vectors

Elements \(\mathbf{v}\) in \(\mathbb{R}^n\) are Vectors. A vector can be thought of as \(n\) real numbers stacked on top of each other (column vectors).

\[\mathbf{v} = \left( \begin{array}{c} v_1\\ v_2\\ \vdots\\ v_n \end{array} \right)\]

Properties of Vectors

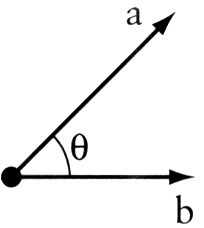
Let \(\mathbf{v}, \mathbf{a}, \mathbf{b}\) be vectors in \(\mathbb{R}^n\), and \(\gamma\) a scalar in \(\mathbb{R}\) . Let \(\theta\) be the angle between vectors A and B.

angle

  • \(\mathbf{v}^T = (v_1, v_2, \dots, v_n)\) is the Transpose of a vector.

  • Vector Addition:

\[\mathbf{a} + \mathbf{b} := (a_1 + b_1, \dots , a_n + b_n)^T \in \mathbb{R}^n\]
  • Scalar Multiplication:
\[\gamma \mathbf{a} := (\gamma a_1, \dots , \gamma a_n)^T \in \mathbb{R}^n\]
  • The scalar product between two vertices, or Dot Product:
\[\mathbf{a} \cdot \mathbf{b} := \sum_{i=1}^{n} a_i b_i \in \mathbb{R}\]

The scalar product is also written as \((\mathbf{a},\mathbf{b})\) or as \(\mathbf{a}^T\mathbf{b}\). The scalar product is Symmetric. That is, \(\mathbf{a} \cdot \mathbf{b} = \mathbf{b} \cdot \mathbf{a}\)

  • The vector Norm or length of a vector is defined by
\[\| \mathbf{v} \| := \sqrt{\mathbf{v} \cdot \mathbf{v}} = \sqrt{\sum_{i=1}^{n} v_i^2}\]

There are different “kinds” of norms. This particular norm is called the Euclidean Norm for a vector. More information on norms can be found here.

  • Cauchy-Bunyakowski-Schwarz Inequality: The following inequality holds:
\[\mathbf{a} \cdot \mathbf{b} \leq \| \mathbf{a} \| \| \mathbf{b} \|\]
  • Triangle Inequality: The following inequality holds:
\[\| \mathbf{a} + \mathbf{b} \| \leq \| \mathbf{a} \| + \| \mathbf{b} \|\]
  • The cosine of the angle \(\theta\) between vectors \(\mathbf{a}\) and \(\mathbf{b}\) is \(\cos{\theta} := \frac{\mathbf{a} \cdot \mathbf{b}}{\| \mathbf{a} \| \| \mathbf{b} \|}\)
  • \(\mathbf{a} \perp \mathbf{b}\) means the vectors \(\mathbf{a}\) and \(\mathbf{b}\) are Orthogonal. The following is true:

\(\mathbf{a} \perp \mathbf{b} \Leftrightarrow \mathbf{a} \cdot \mathbf{b} = 0 \Leftrightarrow \cos{\theta}=0\) \(\mathbf{v} \perp \mathbf{v} \Leftrightarrow \mathbf{v} = 0\)

Definitions of Vertices

  • A linear subspace \(L \subseteq \mathbb{R}^n\) is a set enjoying the following properties:
    • For all \(\mathbf{a}\), \(\mathbf{b} \in L\) it holds that \(\mathbf{a} + \mathbf{b} \in L\)
    • For all \(\mathbf{a} \in L\), \(\gamma \in \mathbb{R}\) it holds that \(\gamma + \mathbf{a} \in L\)
  • An affine subspace \(A \subseteq \mathbb{R}^n\) is any set that can be represented as \(\mathbf{v} + L := \{ \mathbf{v} + \mathbf{x} : \mathbf{x} \in L\}\), for some vector \(\mathbf{v}\) in \(\mathbb{R}^n\) and linear subspace \(L \subseteq \mathbb{R}^n\)
  • A set of vectors \((\mathbf{v_1}, \mathbf{v_2}, \dots, \mathbf{v_n})\) is said to be Linearly Independent if and only if
\[\sum_{i=1}^{n} \gamma_i \mathbf{v_i} = \mathbf{0}^n \text{ implies } \gamma_1 = \gamma_2 = \dots = \gamma_n = 0\]

There can be at most \(n\) linearly independent vectors in \(\mathbb{R}^n\). Orthogonal vectors are also linearly independent. Linearly independent vectors are not necessarily orthogonal.

  • Any collection of \(n\) linearly independent vectors is called a Basis.
    • A basis is said to be Orthogonal Basis if \(\mathbf{v_i} \perp \mathbf{v_j}\) for all vectors in the collection
    • A basis is said to be an Orthonormal Basis if \(\| \mathbf{v_i} \| = 1\)
    • The Standard Basis is the collection of orthonormal vectors \((e_1, e_2, \dots , e_n)\) such that \(e_{i_j} = \begin{cases}1 & i = j \\ 0 & \text{otherwise} \end{cases}\). The vectorspace \(\mathbb{R}^n\) is equipped with the standard basis.

Matrices

Consider two spaces \(\mathbb{R}^n\) and \(\mathbb{R}^k\). All linear functions from \(\mathbb{R}^n\) to \(\mathbb{R}^k\) may be described using a linear space of Real Matrices \(\mathbb{R}^{k \times n}\) .

\[{\bf A} = \underbrace{ \left.\left( \begin{array}{ccccc} 1,1&1,2&1,3&\cdots &1,n\\ 2,1&2,2&2,3&\cdots &2,n\\ 3,1&3,2&3,3&\cdots &3,n\\ \vdots&&&\ddots&\\ k,1&k,2&k,3&\cdots &k,n \end{array} \right)\right\} }_{n\text{ columns}} \,k\text{ rows}\]

Properties of Matrices

Let \(A \in \mathbb{R}^{k \times n}\) and \(B \in \mathbb{R}^{n \times m}\), and \(\gamma\) a scalar in \(\mathbb{R}\) . Let \(\mathbf{v} \in \mathbb{R}^n\) and \(\mathbf{u} \in \mathbb{R}^k\)

  • \(A^T\) is the Transpose of a matrix.
    • \(A^T_{ij} := A_{ji}\) .
    • \((A^T)^T = A\) .
    • \((AB)^T = B^T A^T\) .
  • Matrix Addition:
\[(A + B)_{ij} := A_{ij} + B_{ij}\]
  • Scalar Multiplication:
\[(\gamma A)_{ij} := \gamma A_{ij}\]
  • Matrix Multiplication: Let \(A \in \mathbb{R}^{k \times n}\) and \(B \in \mathbb{R}^{n \times m}\). Then
\[(A B)_{i j} := \sum_{l=1}^{n} A_{il} B_{lj} \in \mathbb{R}^{k \times m}\]

Matrix multiplication is tricky and should be seriously practiced. Matrix multiplication is Associative (meaning \((A B) C = A (B C)\)), but it is Non-Commutative (meaning \(A B\) may not equal \(B A\)).

  • Let \(\mathbf{v} \in \mathbb{R}^n\) be a vector. Than \(\mathbf{v} \cong V\) where \(V \in \mathbb{R}^{n \times 1}\)

  • The Norm of a matrix is defined by

\[\| A \| := \sqrt{\sum_{i=1}^{n} \sum_{j=1}^{n} A_{i j}^2} = \max(\|A \mathbf{v} \|) \text{ where } \mathbf{v} \in \mathbb{R}^n : \| \mathbf{v} \| = 1\]
  • There are different “kinds” of matrix norms. This norm is the Frobenius, or 2-norm. More information on norms can be found here.
    • \(\| A \| = \| A^T \|\) .
    • Triangle Inequality: \(\| A + B \| \leq \| A \| + \| B \|\)

Matrix Definitions

  • The Range or Range Space of a matrix is defined as
\[\text{range}(A) := y \in \mathbb{R}^m : y = Ax \text{ for some } x \in \mathbb{R}^n\]
  • The Kernel or Null Space of a matrix is defined as
\[\text{ker}(A) := x \in \mathbb{R}^n : Ax = 0^m\]

The kernel and the range of a matrix are subspaces of \(\mathbb{R}^{n \times m}\)

  • The Rank of a matrix is defined as the minimum of the dimensions of the range space of \(A\) and the range space of \(A^T\).
    • \(\text{rank}(A) = \text{rank}(A^T)\) .
    • A matrix is said to have Full Rank if the rank of \(A\) equals \(\min\{ n, m\}\)
    • The rank of a matrix is also equal to the number of Pivot Points it has when reduced. This video explains more.

Square Matrices

Square Matrices have additional unique properties. Let \(A \in \mathbb{R}^{n \times n}\)

  • The determinate of a square matrix is a special number with unique properties. The determinate of a \(2 \times 2\) matrix \(B\) is calculated by
\[\det\left( \begin{array}{cc} a&b\\ c&d \end{array} \right) := a d - b c\]

calculating the determinate of larger matrices is more complex, but a nice tutorial can be found here.

  • There exists the Identity Matrix \(I\) such that
\[I := \left( \begin{array}{ccccc} 1&0&0&\cdots &0\\ 0&1&0&\cdots &0\\ 0&0&1&\cdots &0\\ \vdots&&&\ddots&\\ 0&0&0&\cdots &1 \end{array} \right)\]
  • If \(A \mathbf{v} = \gamma \mathbf{v}\) holds for some vector \(\mathbf{v} \in \mathbb{R}^n\) and scalar \(\gamma \in \mathbb{R}\), then we call \(\mathbf{v}\) a Eigenvector of \(A\), and we call \(\gamma\) an Eigenvalue of \(A\).
    • The set of Eigenvectors of \(A\), corresponding to their eigenvalues, form a linear subspace of \(\mathbb{R}^n\)
    • Every matrix \(A \in \mathbb{R}^{n \times n}\) has \(n\) eigenvalues (counted with multiplicity). Eigenvalues may be complex.
    • The sum of the \(n\) eigenvalues of \(A\) is the same as the Trace of \(A\) (that is, the sum of the diagonal elements of \(A\)).
    • The product of the \(n\) eigenvalues of \(A\) is the determinate of \(A\)
    • The roots of the Characteristic Equation \(\det(A-\lambda I)\) are the eigenvalues of A.
    • The norm of A is at least as large as the largest absolute value of it’s eigenvalues.
    • The eigenvalues of \(A^{-1}\) are the inverses of the eigenvalues of \(A\)
    • for square matrices, the eigenvalues of \(A^T\) are the eigenvalues of \(A\)
  • For a square matrix \(A\) there can exist an Inverse Matrix \(A^{-1}\), with \(A A^{-1} = I\)
  • A invertible square matrix is called Nonsingular. Nonsingular matrices have the following properties, and the following properties imply a matrix is nonsingular:
    • There exists it’s inverse, \(A^{-1} : A A^{-1} = I\)
    • The rows and columns of \(A\) are linearly independent.
    • The system of linear equations \(A x = \mathbf{v}\) has a unique solution for all \(\mathbf{v} \in \mathbb{R}^n\).
    • The homogenous system of equations \(A x = 0^{n}\) has only one solution, \(x = 0^n \in \mathbb{R}^n\).
    • \(A^T\) is nonsingular.
    • \(\det(A) \neq 0\) .
    • None of the eigenvalues of \(A\) are 0.
  • The set of all nonsingular \(n \times n\) square matrices forms a Ring. This ring is non-commutative, and is therefore closed under addition and matrix multiplication.
  • We call \(A\) Symmetric if and only \(A^T = A\). Symmetric matrices have the following properties:
    • \(A_{ij} = A_{ji}\) .
    • Eigenvalues of symmetric matrices are real.
    • Eigenvectors corresponding to distinct Eigenvalues are orthogonal to each other.
    • The norm of a symmetric matrix equals the largest absolute value of it’s eigenvalues.
    • Even if \(X\) is a non-square matrix, \(X^T X\) and \(X X^T\) are square symmetric matrices.
      • If the columns of \(X\) are linearly independent, then \(X^T X\) is nonsingular.
      • If the columns of \(X^T\) are linearly independent, then \(X X^T\) is nonsingular.
      • The eigenvalues of \(X^T X\) and \(X X^T\) are the same, and are non-negative.
  • We call \(A\) a Positive Definite matrix if and only if for all \(\mathbf{v} \in \mathbb{R}^n\), \(\mathbf{v} \cdot A \mathbf{v} > 0\). We represent this with \(A \succ 0\)
    • Respectively, we call \(A\) a Negative Definite matrix, and \(A \prec 0\) if and only if \(\mathbf{v} \cdot A \mathbf{v} < 0\)
    • Respectively, we call \(A\) a Negative Semidefinite matrix, and \(A \preceq 0\) if and only if \(\mathbf{v} \cdot A \mathbf{v} \mathbf{\leq} 0\)
    • Respectively, we call \(A\) a Positive Semidefinite matrix if, and \(A \succeq 0\) and only if \(\mathbf{v} \cdot A \mathbf{v} \mathbf{\geq} 0\)
    • \(A\) is positive definite if and only if it has positive eigenvalues
      • Respectively \(A\) is negative definite if and only if it has negative eigenvalues
      • Respectively \(A\) is positive semidefinite if and only if it has non-negative eigenvalues
      • Respectively \(A\) is negative semidefinite if and only if it has non-positive eigenvalues
    • For symmetric matrices \(A\) and \(B\), \(A \succeq B\) if and only if \(A - B \succeq 0\)
      • Respectively \(A \succ B\) if and only if \(A - B \succ 0\)
    • The sum of two positive definite matrices is also positive definite.
    • Every positive definite matrix is nonsingular and invertible, and it’s inverse is also positive definite
    • If \(A\) is positive definite and real \(r > 0\), then \(rA\) is positive definite
  • Let \(A\in\mathbb{R}^{n \times n}\) be a symmetric matrix. Then the determinant
\[\bigtriangleup_k = \begin{align}\begin{bmatrix} a_{1 1}& \dots & a_{1 k}\\\vdots & \ddots & \vdots \\ a_{k 1} & \dots & a_{k k} \end{bmatrix} \end{align}\]

for \(1 \leq k \leq n\) is called the k-th principal minor of A.

  • If \(A\in\mathbb{R}^{n \times n}\) is a symmetric matrix, and if \(\bigtriangleup_k\) is the k-th principal minor for \(k = 1, \dots, n\) then
    • \(A\) is positive definite if \(\bigtriangleup_k > 0\)
    • \(A\) is negative definite if \((-1)^k \bigtriangleup_k > 0\). That is, the principal minors alternate sign starting with \(\bigtriangleup_1 < 0\)
    • If either of the above conditions applied for all but \(\bigtriangleup_n = 0\), then \(A\) is semidefinite.

###Sources

@book{andréasson2005introduction,
  title={An Introduction to Continuous Optimization},
  author={Andr{\'e}asson, N. and Evgrafov, A. and Patriksson, M.},
  isbn={9789144044552},
  url={https://books.google.com/books?id=dxdCHAAACAAJ},
  year={2005},
  publisher={Professional Publishing Svc.}
}
@misc{ wiki:xxx,
   author = "Wikipedia",
   title = "Positive-definite matrix --- Wikipedia{,} The Free Encyclopedia",
   year = "2016",
   url = "https://en.wikipedia.org/w/index.php?title=Positive-definite_matrix&oldid=700197014",
   note = "[Online; accessed 17-January-2016]"
 }